Ao longo da sua vida Leonhard Euler teve treze filhos e quando faleceu, em 1783, estava cego.  Mas a cegueira não o impediu de trabalhar e grande parte dos cerca de 1000 livros e artigos científicos que escreveu foram produzidos quando já se encontrava nessa condição.

Em 1735 Euler resolveu um desafio matemático e lógico conhecido como o Problema das Sete Pontes de Königsberg.

A cidade de Königsberg na Prússia (actual Kaliningrado na Rússia) foi construída ao longo dos dois lados do rio Prególia e incluía duas grandes ilhas que estavam ligadas entre si, e ao continente, por sete pontes. O problema consistia em encontrar uma rota pela cidade que cruzasse cada ponte uma e apenas uma vez.

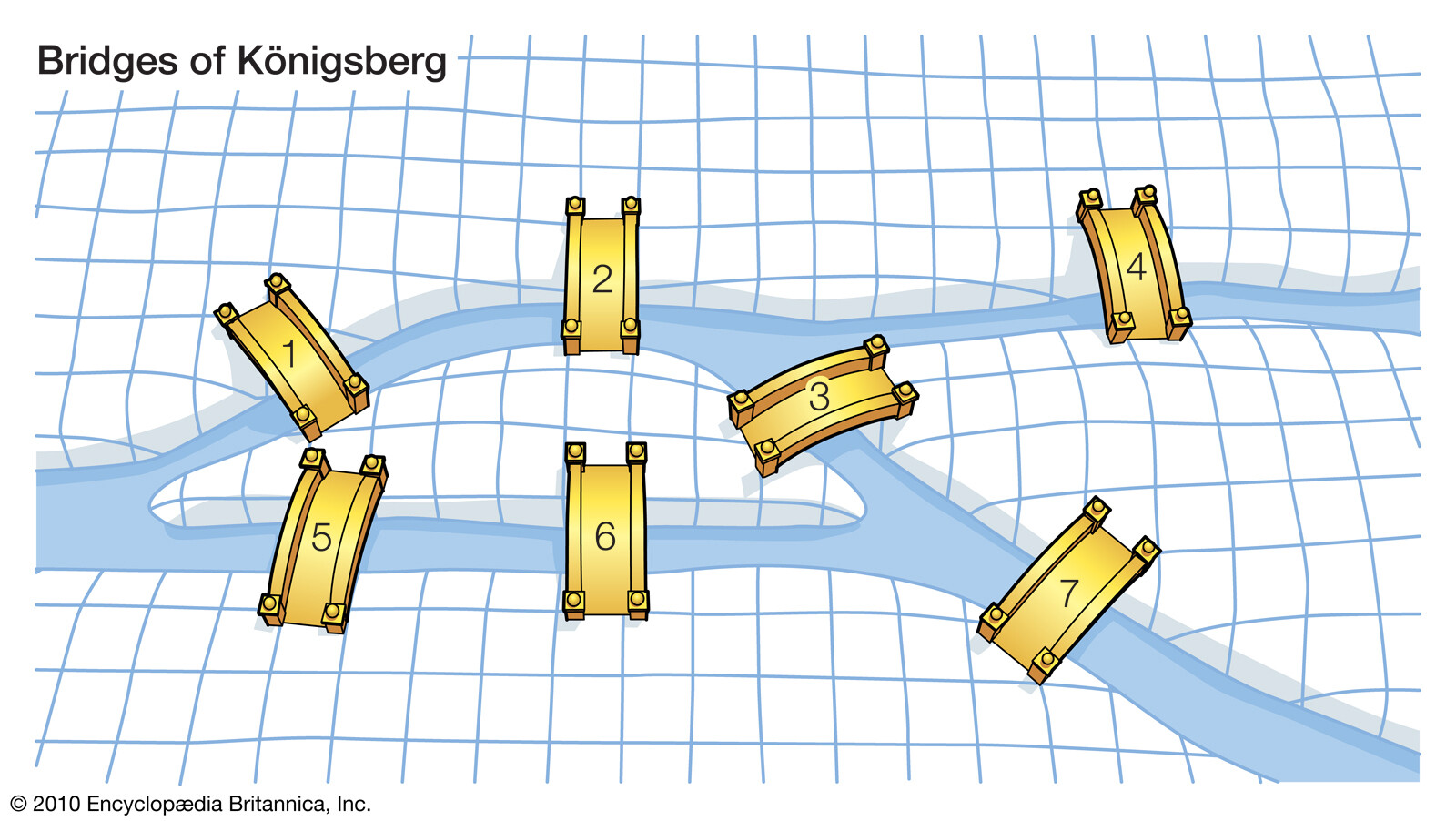
Figura 1 - Konigsberg e as suas 7 pontes fonte: https://www.britannica.com/science/Konigsberg-bridge-problem

Tome alguns momentos para tentar desenhar uma rota que atravesse cada uma das pontes a verde, começando e terminando onde quiser, mas deve atravessar todas as pontes e não mais do que uma vez.

O método que Euler utilizou para resolver este problema é algo mais importante do que a própria solução.

Ele começou por reparar que a escolha da rota dentro de cada uma das quatro zonas de terra não interessa para nada. A única característica importante é a sequência em que decidimos passar as pontes.

Esta ideia permitiu-lhe formular o problema em termos abstractos, ou seja, substituiu cada zona de terra por um nó abstracto e cada ponte por uma conexão abstracta entre dois nós.

Ao fazer isto, Euler criou uma importante estrutura matemática, aquilo que hoje conhecemos como “grafo”.

Um grafo é uma representação pictórica composta por pontos (vértices) ligados por linhas (arestas), que podem de alguma forma ser distorcidas sem alterar o próprio grafo.

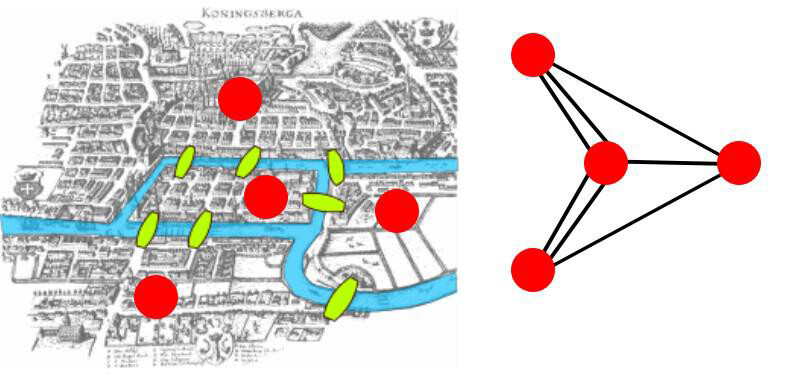
Figura 2 - Representação enquanto grafo Fonte: https://universoracionalista.org/origem-da-teoria-dos-grafos-as-7-pontes-de-konigsberg

Ao considerarmos o grafo dispensamos a imagem. Podemos trabalhar o problema de forma mais abstracta.

Este processo de criar um modelo matemático da realidade que observamos é algo a que chamamos de “modelação”. Habitualmente, quando implementamos um sistema de optimização de rotas fazemos uma análise de todas as regras e restrições que influenciam a criação de uma qualquer sequência de visitas para uma frota. Ou seja, modelamos matematicamente para em seguida aplicarmos algoritmos matemáticos que resolvem o problema da determinação das rotas para cada veículo.

Dessa forma, Euler foi capaz de deduzir que se partir de um vértice com um número ímpar de arestas então não poderá terminar nele caso queira percorrer todas as arestas uma vez só. Por exemplo, se tenho 3 arestas, saio por uma, regresso por uma segunda, volto a sair pela terceira e já não tenho mais arestas para poder regressar. Por isso terei de terminar o percurso noutro vértice qualquer.

Por outro lado, o grafo só pode ter dois vértices com um número ímpar de arestas, um para começar e o outro para terminar o percurso, ou então não pode ter nenhum.

Repare que nos últimos parágrafos só temos utilizado a linguagem da modelação matemática falando em vértices e arestas, já não estamos a falar daquilo que representam, as zonas de terra e as pontes. É precisamente este efeito que Euler conseguiu introduzir, o de enunciarmos teorias e algoritmos em função de conceitos abstractos que podem ser aplicados a qualquer problema da realidade.

Por isso, ao voltarmos à linguagem da realidade, podemos concluir que como as quatro zonas de terra no problema original são tocadas por um número ímpar de pontes, a existência de um caminho que atravessa cada ponte uma vez só leva inevitavelmente a uma contradição.

E como tal o problema não tem solução.

Por outro lado, se Königsberg tivesse uma ponte a menos, ou uma ponte a mais, então uma solução teria sido possível. Deixo-o com o exercício de o experimentar.

Curiosamente, quem veio a resolver este problema definitivamente foi a força aérea aliada durante a segunda grande guerra mundial. Os bombardeamentos da cidade destruíram duas pontes e resolveram o problema até aos dias de hoje. Mas talvez não da melhor forma.

A teoria dos grafos e o problema da determinação de um caminho Euleriano num grafo levaram à constatação de outro problema curioso. E se em vez de querermos passar por todas as arestas quiséssemos passar por todos os vértices?

Ou seja, o problema já não é passar por todas as pontes, mas sim por todas as zonas de terra uma e uma só vez. A esse caminho chamamos de Hamiltoniano em nome de William Hamilton.

Por sua vez, o problema do caminho Hamiltoniano levou à enunciação do problema do caixeiro-viajante. Este supõe que um vendedor ambulante (caixeiro-viajante) pretende visitar um conjunto de cidades (vértices) passando por cada cidade uma vez e retornando à cidade de origem, onde dorme no final do dia, fazendo o caminho de menor comprimento possível.

O problema do caixeiro-viajante é hoje em dia utilizado para determinar a rota de muitas viaturas que encontramos na estrada, e que seguem um plano pré-concebido de visitas.

As técnicas desenvolvidas para resolver este problema evoluíram ao longo das últimas décadas para dar origem aos mais avançados algoritmos de planeamento e optimização de rotas considerando frotas inteiras, não apenas veículo a veículo.

Estes algoritmos são hoje utilizados por milhares de empresas de logística em todo mundo. São eles que definem as rotas que os camiões que vemos na rua seguem desde os armazéns de onde partiram até chegar ao café, ao supermercado, ao banco, a todos os locais onde vamos. Ou íamos.

Tags